能力育成問題集13/積み木の数②
四則演算のすべての基礎
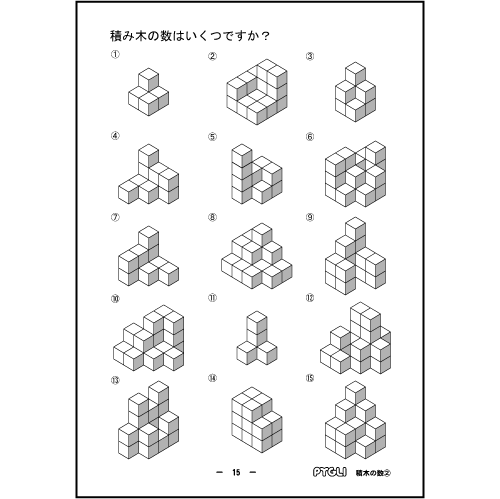
「積み木の数①」よりも問題の数が増え、積まれた積み木の数も増えています。数能力向上のため、さらにたくさんの問題にチャレンジしてください。
積み木を自在に分割し、集合体として瞬時に数を認識することで、四則演算のすべての基礎が育成されます。この問題は数能力全般の能力育成に効果的で、特に事象の抽象化・概念化の能力育成に効果を発揮します。問題に取り組む際は、単純に1,2,3,・・・と数えさせず、数をまとまりとしてとらえる練習をさせてください。
「積み木の問題」「積み木の数①」と一緒に取り組めば、確実に数能力がアップしていきます。無理をせず、一日数問ずつこなしていきましょう。
数を瞬時にとらえるための指導法(1)
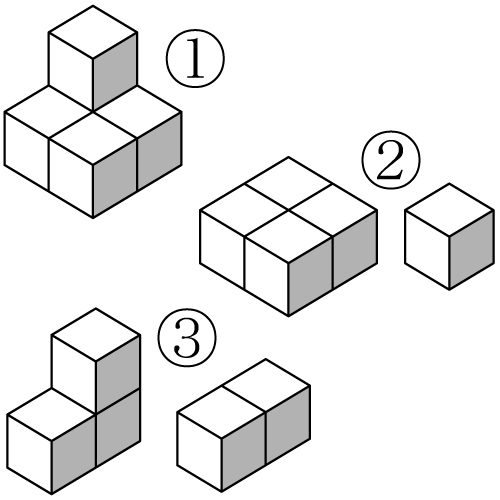
①の積み木は5個ですが、1つは下段の後ろに隠れて見えません。しかし、②のように4個と1個に分解できますし、③のように3個と2個にも分解できます。これらを合成すれば、どれでも合計が5個になることがわかります。
指導の際は、②の場合は4個のかたまりを指でつまんで「4個と」と言い、次に1個のかたまりをつまんで「4個と1個で5個」と言ってください。
③の場合は3個のかたまりを指でつまんで「3個と」と言い、次に2個のかたまりをつまんで「3個と2個で5個」と言ってください。
数える際はどちらの分割方法でもいいですが、最終的にどれもが同時に見ることができるようになって、はじめて数を瞬時にとらえるという目的が達成されるのです。
数を瞬時にとらえるための指導法(2)
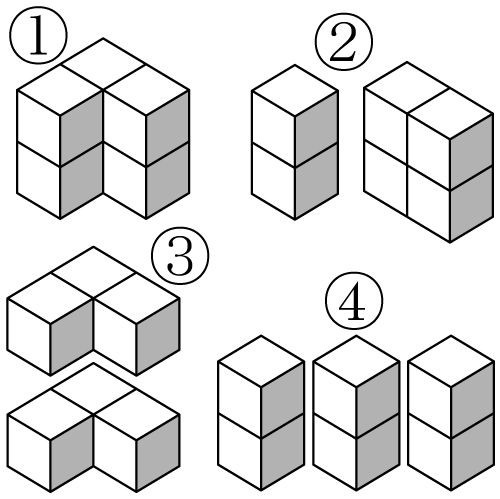
①の積み木は6個ですが、1つは下段の後ろに隠れて見えません。しかし、②のように4個と2個に分解できますし、③のように3個と3個にも分解できます。さらに、④のように2個と2個と2個にも分解できます。これらを合成すれば、どれでも合計が6個になることがわかります。
以上のすべてを、同時に、全体的に見て、感じるのです。
数を瞬時にとらえるための指導法(3)
①の積み木は8個ですが、2つは下段の後ろに隠れて見えません。これは6個と2個に分解できますし、5個と3個にも分解できます。これらを合成すれば、どれでも合計が8個になることがわかります。
②の積み木は9個ですが、2つは下段の後ろに隠れて見えません。これは8個と1個に分解できますし、5個と4個にも分解できます。さらに4個と5個にも分解できます。これらを合成すれば、どれでも合計が9個になることがわかります。
目の錯覚により、後ろに積み木が存在しているように見えるときがあります。存在していない積み木は数に入りませんので、積まれた積み木の構成を三次元で考えるようにしてください。
ウッディブロックのような実物を使って、積まれた積み木を実際に分割して読み取りができるようにしてください。ある程度こなせるようになったら、「積み木の数①」「積み木の数②」を使い、積まれた積み木を瞬時に読み取らせてください。
「積み木ブロック推理①」「積み木ブロック推理②」「積み木ブロック推理③」も同時に取り組めば、さらに効果的です。